
In such case, we should probably look for better predictor variables. A low correlation (-0.2 < x < 0.2) probably suggests that much of variation of the outcome variable (y) is not explained by the predictor (x). Its value ranges between -1 (perfect negative correlation: when x increases, y decreases) and +1 (perfect positive correlation: when x increases, y increases).Ī value closer to 0 suggests a weak relationship between the variables.

The correlation coefficient measures the level of the association between two variables x and y. It’s also possible to compute the correlation coefficient between the two variables using the R function cor(): cor(marketing$sales, marketing$youtube) # 0.782 This is a good thing, because, one important assumption of the linear regression is that the relationship between the outcome and predictor variables is linear and additive. The graph above suggests a linearly increasing relationship between the sales and the youtube variables. Ggplot(marketing, aes(x = youtube, y = sales)) + Create a scatter plot displaying the sales units versus youtube advertising budget.A non-zero beta coefficients means that there is a significant relationship between the predictors (x) and the outcome variable (y). Once, the beta coefficients are calculated, a t-test is performed to check whether or not these coefficients are significantly different from zero. This method of determining the beta coefficients is technically called least squares regression or ordinary least squares (OLS) regression. Mathematically, the beta coefficients (b0 and b1) are determined so that the RSS is as minimal as possible. Since the mean error term is zero, the outcome variable y can be approximately estimated as follow: This is one the metrics used to evaluate the overall quality of the fitted regression model.

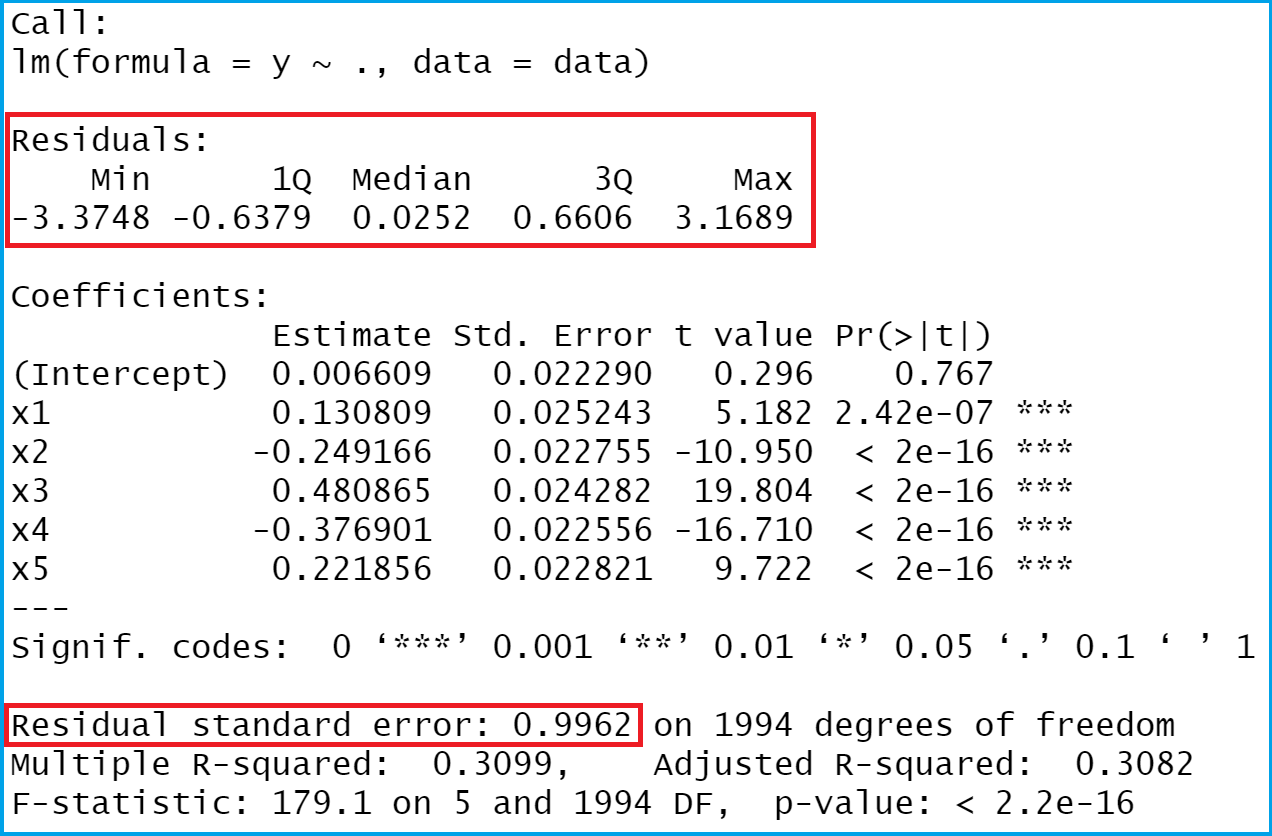
The average variation of points around the fitted regression line is called the Residual Standard Error ( RSE). The sum of the squares of the residual errors are called the Residual Sum of Squares or RSS. Some of the points are above the blue curve and some are below it overall, the residual errors (e) have approximately mean zero.
b1 is the slope of the regression line.b0 is the intercept of the regression line that is the predicted value when x = 0.b0 and b1 are known as the regression beta coefficients or parameters:.The mathematical formula of the linear regression can be written as y = b0 + b1*x + e, where:


 0 kommentar(er)
0 kommentar(er)
